
Accuracy Leads to Perfection
Woodz Co. had given the Syndicate a surprise test in the form of a lab called, "Projectile Bull’s-eye." This was a heart-breaking experience as we, the Syndicate experienced our first failure as a group and had no way of redeeming ourselves because this was a one and done type of task. Thankfully, it was only a test, an opportunity to learn and not a pivotal task in which we were actually working in the field. The Most important lesson we learned from this task was that accuracy leads to perfection.
In this task, we had to calculate the distance which we had to place a bull’s-eye so ball bearing could hit the bull’s-eye. There were two phases in the task. First, we had the mechanical energy phase. In the energy phase, we were given a ramp and a photo-gate, an instrument which would help us determine the time it takes for a ball to move through a small distance. Furthermore, during the test, we were going to be given a random height on the ramp from where the ball would be released. The tough part was that the ramp had friction; therefore, in the energy phase, the ball would lose energy.
What we knew from our energy concepts were that mechanical energy is cannot be created, it is only transferred. We learned about two types of energy for this lab, gravitational potential energy and kinetic energy. In ideal situations, when there is no movement and an object has height, it has gravitation potential energy; for example, if we were to observe from the ground and look at a ball being dropped from a building, right before it starts falling, the ball has only gravitational potential energy. This gravitational potential energy can be expressed through the equation, E=mgh, where E is energy, m is mass, g is acceleration due to gravity, and h is the height.
We also learned about kinetic energy. Kinetic energy is existant when there is movement; that is to say, an object has a velocity. Kinetic energy can be expressed as E=0.5mv^2 For example, when a ball is rolling down a slope, it has kinetic energy; however, the ball also has potential energy. The relationship between gravitational potential energy, kinetic energy, and total mechanical energy can be expressed through the equation: Etotal=Egravitational potential + Ekinetic. Therefore, as an object gains velocity and loses height, the object's gravitational potential energy is being transformed into kinetic energy and as an object gains height, it is gaining gravitational potential energy.
We learned all of this with ideal conditions; that is to say, there was no energy loss; however, in this lab, energy was going to be lost due to friction and we had to determine the amount of energy lost due to friction per square unit in order to determine the best location to place the bull’s-eye. After doing some calculations, we hypothesized that the bull's-eye should be 1.11m from the launch position.
Roles
Project Managers: Parth
Project Documenters: Jasmit
Project Webmaster: Parth
Project Facilitator: Jasmit
Project Timekeepers: Parmveer
Picture Taking: Gurjot
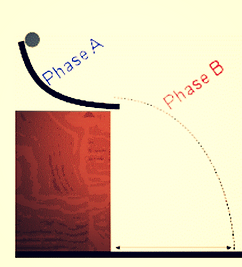
A brief diagram of the task.

The ramps that were used.
Materials
• ball bearing
• carbon paper
• dynamics ramp
• explorer
• masking tape
• metre stick
• photo gates
• plumb bob
• ramp
• string
• target sheet
Procedure
1. Placed the motion gate at the end of the ramp
2. Placed the dynamics where the front of the ramp is right where the photo gates are activated
3. Measured the diameter of the ball bearing
4. Rolled the ball bearing from the top of the dynamics ramp at least 5 times
5. Recorded the time from the explorer
6. Calculate the average time it takes for the ball bearing to pass the photo gate
7. Calculated the velocity of the ball bearing at the end of the ramp.
8. Used the projectile motion formulas to find the horizontal distance where the target sheet can be placed so the ball bearing hits the target and placed the carbon paper on the target sheet
9. Moved the ramp to the end of the table, set the target sheet at derived distance in above step
10. Ran the ball bearing down the ramp and observed the ball bearing
11. Removed the carbon paper from the target sheet and recorded the marked position
Observations and Calculations
Click on Slideshow to see full-size images

Not on the paper, is a 5.



Not on the paper, is a 5.
The Calculations (might have to zoom in to see)
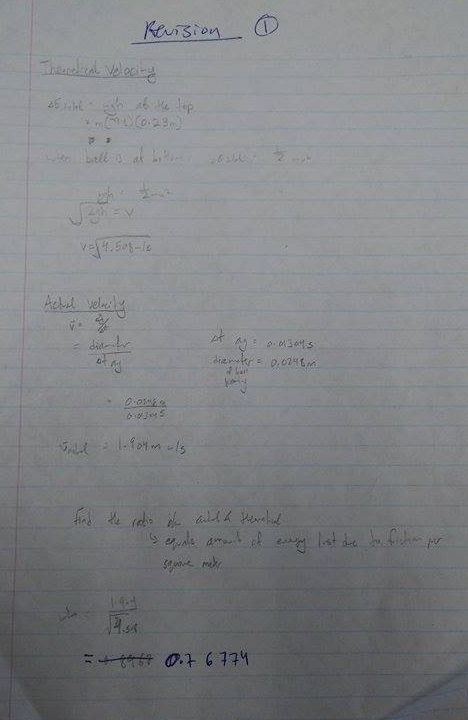
Click image to see full-size
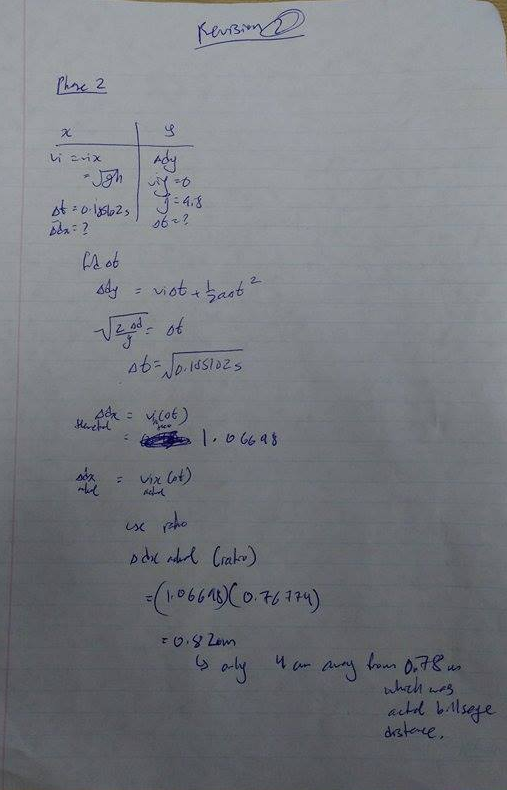

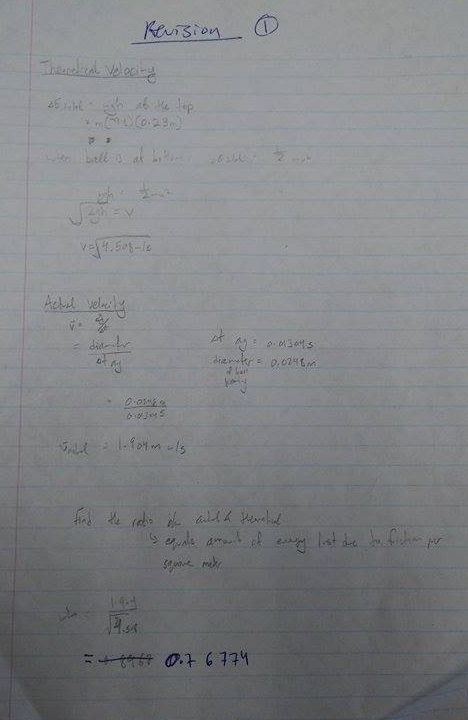
Click image to see full-size
Analysis and Discussion
We had predicted that the distance the ball bearing would land from the launch point would be 1.11m. However, we were wrong. The ball landed 0.78 m from the landing position.
Our initial calculation:
1st, we calculated the distance the ball would move in an ideal system using the conservation of energy equations.
1st, we found the release velocity,
mgh = 0.5mv^2
m(9.8)(0.23)=0.5m(v)^2
rt(2gh) = v
theoretical v = rt4.508m/s
2nd, we found the actual velocity using the cirumference and time on the photogate; however, that was wrong, we should have used diameter, so the correct calculation
average time = 0.01304 s
diameter = 0.078/pi
speed = diameter/time
speed = 1.904 m/s
3rd, we found the ratio between the actual and theoretical velocity
1.904/rt4.508 = 0.76774
Phase 2:
We used kinematics to solve for the distance
since we knew h, we knew vi=rt(gh)
we also knew dy, viy, g
use that information to find time
time = rt(2dy/g)=rt(0.185102)s
then, we used dx = vi(time) to find the displacement
dx = (rt(gh))rt(0.185102)
dx = 0.82 m
0.82 m was only 0.04 m away from our actual result, which was 0.78 m. Therefore, if the correction was made, we would have been a lot more accurate. First, we used circumference instead of diameter to calculate the actual velocity, by doing this, we got a dx of 1.11m which was incorrect. However, using diameter, we got a much more accurate result, with 0.82m.
Although we fixed our calculations, errors still could have occured in this lab. First, their could have been a parallax error, this is because the dynamics ramp was not straight. This could have tampered with the final displacement. Furthermore, instrumental errors could have been made. In order to measure the diameter of the ball bearing, a string was used. A string is only finitely accurate; therefore, it could have resulted in an error being made. Another experiment that can be performed to explain the transfer of energy and related to kinematics is looking at the science behind roller-coasters. Roller-coasters use both energy and kinematics in order to function.
Reflection
You will fail
You will fall
Your effort might be overshadowed by your result
Your failure might be greater than your reputation
But so long as you are determined
And so long as you have heart
You will remain strong
You will not succumb
Keep your love alive
And learn to fly in free-fall
This was a task which was met with failure. We spent days trying to take out our frustration and days trying to get over the failure. No matter what we did, we could not believe that we had failed so bad, there was nothing that could help us. Until, the letter came, it was from Woodz Co. and it said:
We will use this experience as a learning experience and be determined, have heart, and fly in free fall. We will remain a cohesive unit and chase excellence, so we will succeed.
